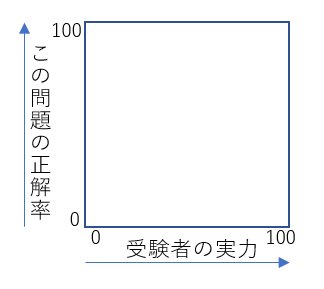
【図1】
数百人の受験者がいたとして、その受験者の『実力』を横軸に、とある1個の問題の正解率を縦軸に取ります。
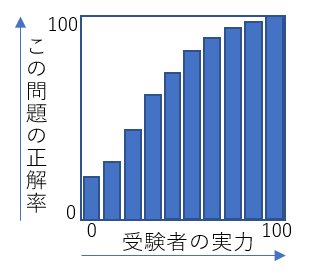
【図2】
上の例だと判りにくいと思うので、受験者を実力で10段階に区切ります。
各段階にはそれぞれ数十人がいるので、その人たちの、その1個の問題の平均正解率を求めて、棒グラフにします。
すると、例えば
←このような感じになります。実力の高い人たちの棒では、問題の平均正解率は高くなるハズです。
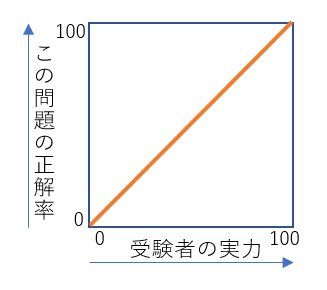
【図3】
現実にはあり得ませんが、『究極の理想の1問』とでも言うものがもしあれば、
←こんな感じのグラフになるかもしれません。
実力の無い人達の平均正解率は0%で、実力満点の人達の平均正解率は100%になり、その間は直線状になります。
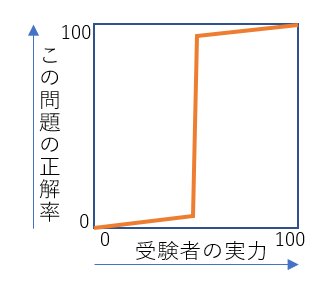
【図4】
こういう問題もあるかもしれません。
実力が、ある閾値を超えたとたんに、正解率が急上昇するような問題です。
『ある程度実力のある人なら、ほぼ間違えないが、実力のない人は、ほぼ解けない』という問題です。
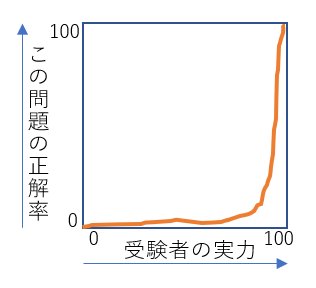
【図5】
こういう傾斜になる問題は、いわゆる『難問』です。実力の相当に高い人だけが正解できます。
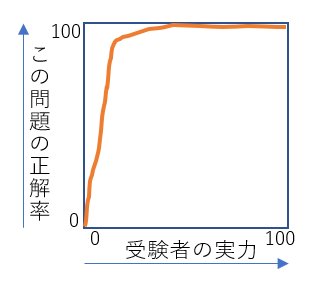
【図6】
こういう傾斜になる問題は、いわゆる『やさしい問題』です。実力の低い人でも正解できます。
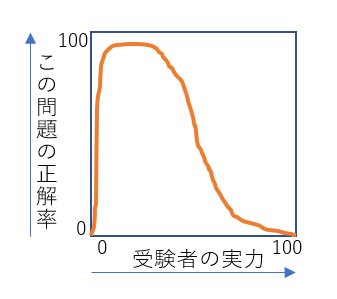
【図7】
この問題は、実力の低い人は正解しやすいのに、実力の高い人は間違ってしまう、という特性をもった問題です。
いわゆる『悪問、奇問』のたぐいです。